3DEXPERIENCE: Piszczenie, skrzypienie, wibracje i drżenie?
Jak mówi książkowa definicja, komfort akustyczny to nic innego jak warunki dobrego samopoczucia. Parafrazując, jest to stan otoczenia będącego w równowadze akustycznej, dzięki której człowiek nie odczuwa negatywnych reakcji, ani zdrowotnych skutków w wyniku emisji niepożądanych dźwięków do otoczenia. Dźwiękami tymi jest w szczególności hałas powstający w trakcie pracy konstrukcji. Okazuje się, że można wspomnianemu zjawisku zapobiec wprowadzając już na etapie projektu wstępnego cyfrowe rozwiązania analityczne pozwalające na analizy strukturalno-akustyczne.
Niestabilność w równaniu ruchu
Za powstaniem niestabilności, które mogą być ujawnione dzięki zastosowaniu procesora pozwalającego na analizę zespolonych wartości własnych, stoi niesymetryczna macierz sztywności i/lub tłumienia. Rzeczywistym przykładem, dla której powyższa sytuacja ma miejsce od strony obliczeniowej, jest tarcie. Piszczenie klocków hamulcowych, dobrze znane kierowcom i pasażerom pojazdów mechanicznych, jest wynikiem wibracji zbudzonych właśnie w wyniku tarcia. Jest to fenomen będący również przedmiotem analizy w niniejszym artykule.
Są dwie drogi pozwalające na przeprowadzenie testu akustycznego pracy zespołu tarcza hamulcowa – klocek hamulcowy – zacisk. Pierwszą z nich jest badanie dynamiczne typu „transient” (przejściowe). Wibracje stowarzyszone z piskiem klocków są za pomocą takiej analizy symulowane bezpośrednio w dziedzinie czasu. Alternatywnym podejściem jest analiza zespolonych wartości własnych, która pod względem czasu przeprowadzania symulacji jest znacznie bardziej wydajna. Gdy rzeczywiste wartości własne układu znajdują się od siebie odpowiednio daleko, nie sprzęgają się w wyniku tarcia – rozwiązanie dynamiczne w zakresie częstotliwości niesprzężonych modów pozostaje stabilne. Co więcej, zespolone wartości własne dla tychże stabilnych modów są ściśle urojone (tarcie ma blisko zerowy wpływ na postacie stabilne). W przypadku gdy rzeczywiste wartości własne układu są blisko siebie, mogą zostać sprzęgnięte w wyniku tarcia. Sprzężone mody tworzą wtedy zespoloną parę o identycznych częściach urojonych oraz przeciwnych częściach rzeczywistych.
Wciskamy środkowy pedał… i co dalej?
Model hamulca jest uproszczoną wersją złożenia hamulca tarczowego najczęściej używanego we współczesnych autach. Składa się on z tarczy oraz pary klocków hamulcowych umieszczonych po obu jej stronach. Klocki wykonane są z organicznego materiału ściernego, tarcza z żeliwa. Płyty podkładowe wykonane są ze stali, a tłumienie materiałowe jest w analizie pominięte.
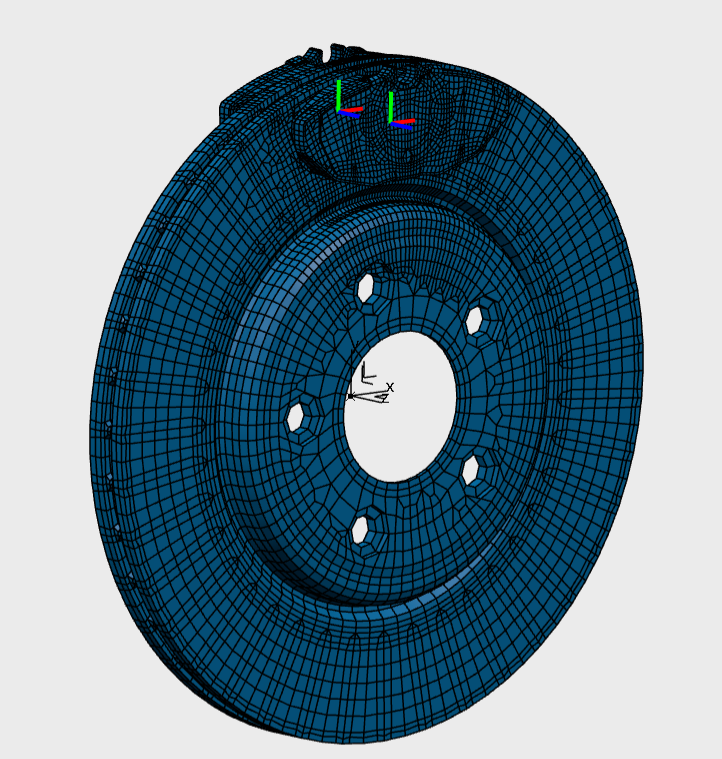
Rozwiązania SIMULIA dostępne na platformie cyfrowej 3DExperience pozwalają na efektywną pracę z modelem dyskretnym. Jednym z wielu dostępnych dla analityka narzędzi jest szybkie tworzenie grup elementów, węzłów, krawędzi, ścian itd. Tym samym w następnych krokach nakładanie warunków brzegowych takich jak siły, ciśnienia, temperatury czy umocowania jest znacznie ułatwione. W omawianym przykładzie zostały utworzony grupy węzłowe, elementowe oraz ścian. Każdą z grup w razie potrzeby możemy wyświetlić w kontekście rozpatrywanego złożenia.
Własności materiałowe zostały przypisane do odpowiednich elementów zawczasu. Komponenty pracuję w zakresie obowiązywania prawa konstytutywnego Hooke’a (materiały liniowe). Na szczególną uwagę zasługują klocki hamulcowe, które modelowane są jako ortotropowe w lokalnym układzie współrzędnych (widoczne na górze rys. 1).
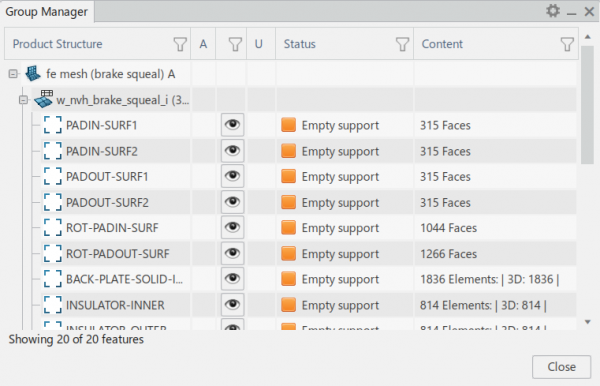
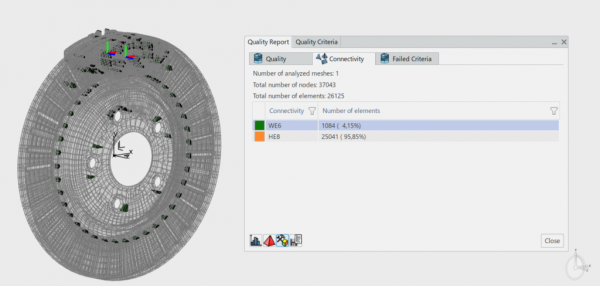
Siatka składa się z elementów bryłowych liniowych typu HEXA (HE8) oraz typu WEDGE (WE6). Obszary w których znajdują się elementy każdego rodzaju zwizualizować możemy za pomocą zakładki „Quality Report” dostępnej w aplikacji do budowy modelu dyskretnego. W tym samym oknie mamy również możliwość podglądu kryteriów jakościowych siatki.
Przeprowadzenie symulacji wymaga od użytkownika zdefiniowania czterech „podkroków”:
- Kroku statycznego w którym przyłożone zostaną obciążenia od ciśnienia na klocki hamulcowe pozwalające na uwzględnienie kontaktu pomiędzy klockami a obracającą się tarczą.
- Drugiego kroku statycznego w którym uwzględniony zostanie ustalony (ang. steady-state) kontakt z tarciem. Kontakt ten jest definiowany poprzez wpisanie prędkości poślizgu w ramach uprzednio określonego pola ruchu. Aby zapobiec nieciągłościom i zapewnić płynne przejście w rozwiązaniu, zerowy współczynnik tarcia jest narzucony w pierwszym kroku; następnie jest zmieniany do żądanej wartości w kroku drugim.
- Ponieważ finalny krok „wyciągania” zespolonych wartości własnych działa w oparciu o metodę tzw. rzutowania podprzestrzeni (ang. subspace projection method) w kroku trzecim użytkownik obowiązany jest przeprowadzić analizę modalną i wyznaczyć rzeczywiste wartości własne.
- Ostatnim etapem jest przeprowadzenie kroku zespolonego, tj. wyznaczenie zespolonych wartości własnych.
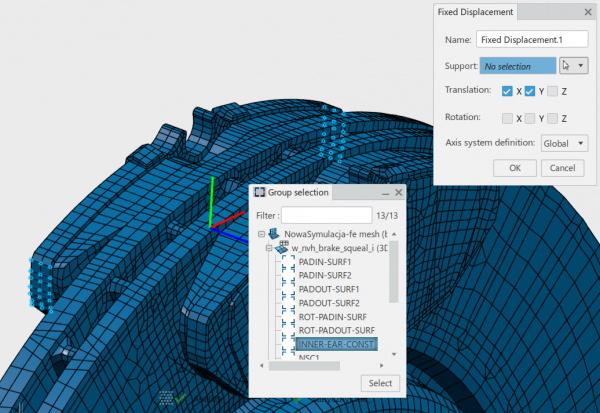
Pierwszy krok statyczny został utworzony w sposób domyślny. W okienku menadżera operacji należy dodatkowo zaznaczyć jednak opcję „Include geometric nonlinearity”. Zdefiniowawszy rodzaj analizy należy przejść do umocowań modelu. Węzłom przedstawionym na rys. 4 odebrano translacyjne stopnie swobody na globalnym kierunku X i Y (zezwalamy na przesuwanie się komponentu w kierunku tarczy). W miejscu ulokowania śrub mocujących odebrano wszystkie stopnie swobody.
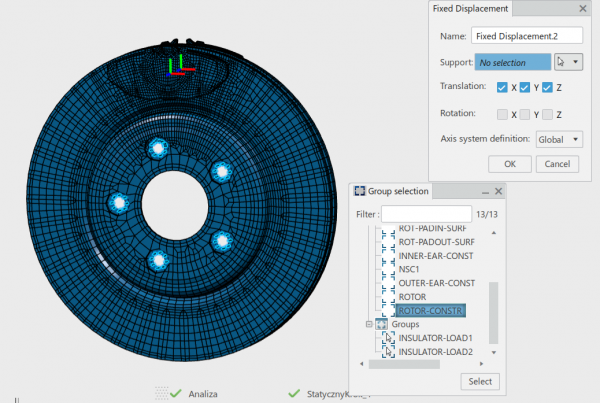
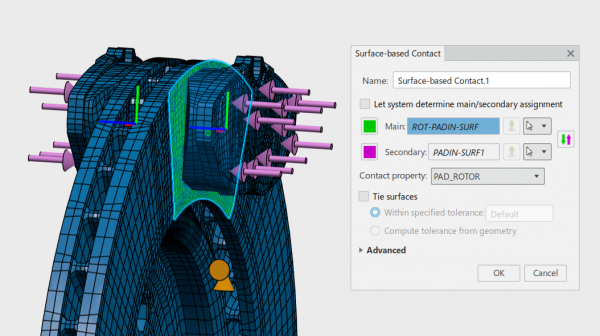
Zacisk działa na układ ciśnieniem o wartości 0.5 MPa w kierunku normalnym do ściany. Należy pamiętać o przyłożeniu obciążenia w sposób symetryczny, jak jest to widoczne na rys. 6. W analizie nałożono następnie własności kontaktu. ABAQUS, będący liderem na rynku solverów obliczeniowych, będący motorem napędowym SIMULIA na platformie chmurowej 3DExperience pozwala na zdefiniowanie kontaktu globalnego, właściwości stycznych, normalnych oraz tłumienia. Dodatkowo użytkownik ma możliwość zastosowania automatycznego, bezodkształceniowego przemieszczenia węzłów celem zetknięcia obiektów, które na etapie modelowania nie zostały do siebie dosunięte. W naszym przypadku zostaną zdefiniowane domyślne właściwości kontaktu oraz ściany stykające się ze sobą. Dostęp do ustawień kontaktu powierzchniowego uzyskamy klikając na ikonkę operacji „Surface-based Contact”. Jak to opisano wyżej posłużono się formułą „małego ślizgu” (ang. small sliding) wraz z metodą dyskretyzacji węzeł do powierzchni. Podobnie przypisano trzy pozostałe, występujące w złożeniu kontakty powierzchniowe. Okno dialogowe przedstawione zostało na rys. 7.
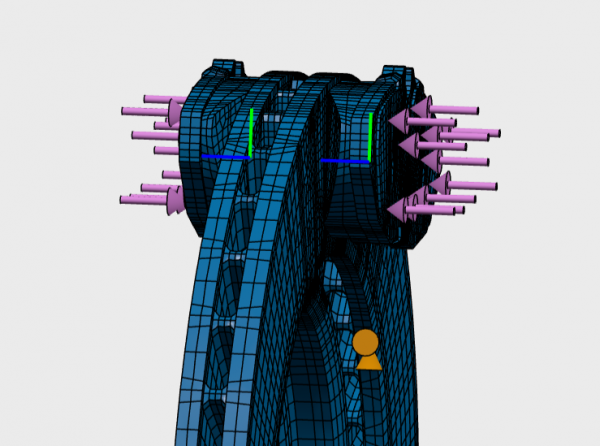
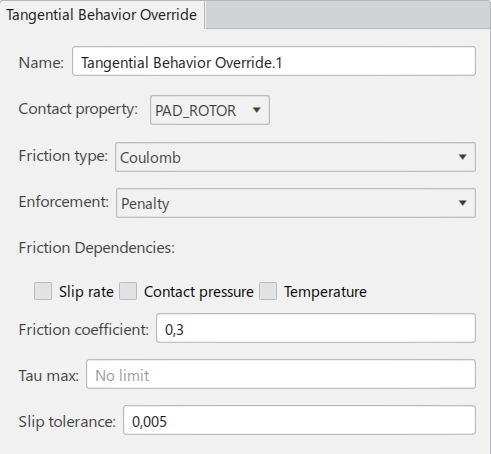
Drugi krok statyczny został zdefiniowany w sposób analogiczny, z domyślnymi ustawieniami. Jedyną różnicą jest nadpisanie zachowania stycznego kontaktu tarciowego. W roli strukturalnej Structural Mechanics Engineer można to zrobić poprzez funkcjonalność „Tangential Behavior Override”. W tym przypadku współczynnik tarcia ma wartość 0.3.
Dalej należy zdefiniować obrotowy ruch tarczy. Symulacja odzwierciedla przypadek hamowania przy niewielkiej prędkości. Aby to zrobić należy wybrać opcję „Sliding Velocity” (prędkość poślizgu) z menu dialogowego pól („Predefined Fields”). Po wybraniu części posiadającej prędkość kątową pozostaje podać wartość prędkości. Arbitralnie nałożono warunek prędkości 5 rad/s uprzednio wybrawszy oś referencyjną.
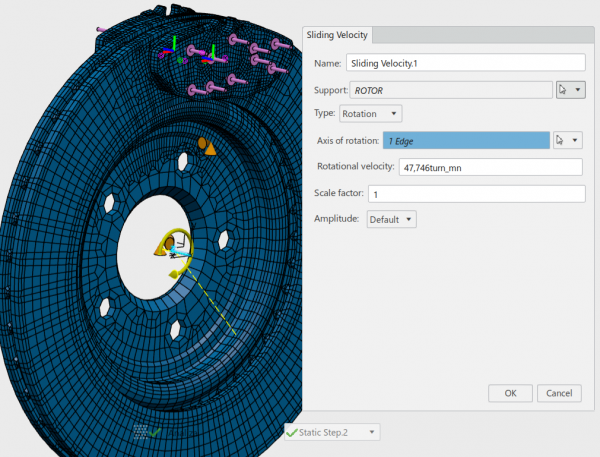
Pora na krok częstotliwościowy. Zdefiniowano metodę Lanczosa, żądając jednocześnie obliczenia 15 modów i wartości własnych drgań własnych. Bezpośrednio po przypisaniu ustawień przypisano, już ostatni, krok pozwalający na przeliczenie zespolonych wartości własnych (ang. „Complex Frequency Extraction Step”). W menadżerze właściwości obrano znowuż 15 modów drgań własnych. Resztę ustawień pozostawiono na wartościach domyślnych. Przez uruchomieniem solvera poddano edycji definicję elementów ośmiowęzłowych na C3D8I. Jest to Abaqusowy element skończony będący usprawnioną wersją C3D8. Usuwa tzw. blokowanie ścinania (shear locking) niwelując sztuczne przesztywnienie konstrukcji. Co więcej, blokowanie objętościowe również jest ograniczone. Efekty takie uzyskiwane są w drodze uzupełnienia „starndardowych” funkcji kształtu o tak zwane funkcje bąbelkowe (ang. „bubble functions”), które mają wartość zerową we wszystkich węzłach i niezerową pomiędzy nimi. Ten rodzaj elementu powinien być stosowany we wszystkich przypadkach, w których elementy liniowe podlegają zginaniu.
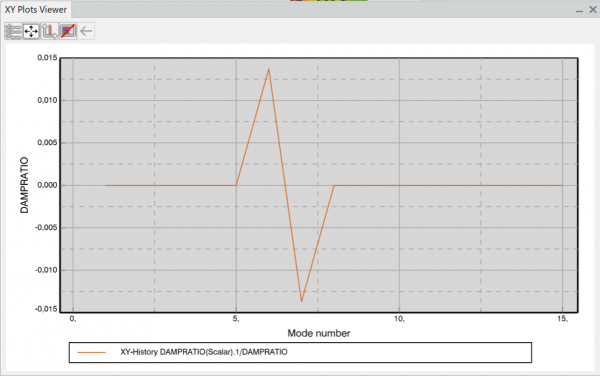
Mody niestabilne charakteryzują się ujemnym współczynnikiem tłumienia. Z panelu umożliwiającego tworzenie wykresów, po wybraniu funkcji X-Y Plot from History (wykres X-Y z historii), wybrać możemy współczynnik tłumienia określony jako DAMPRATIO. Ujemne tłumienie obserwuje się przy modzie 7. Wybierając ostatni krok jesteśmy również w stanie bezproblemowo zweryfikować postać drgań wykorzystując narzędzie do tworzenia animacji.
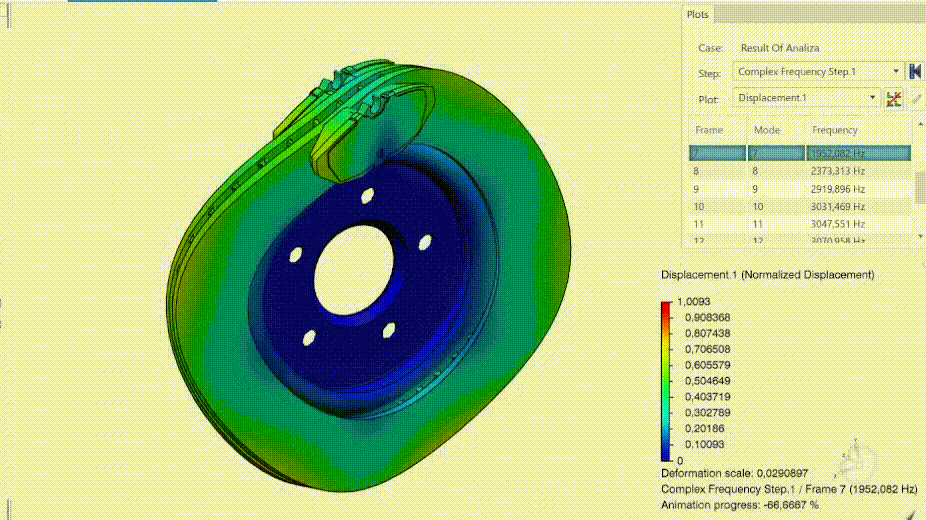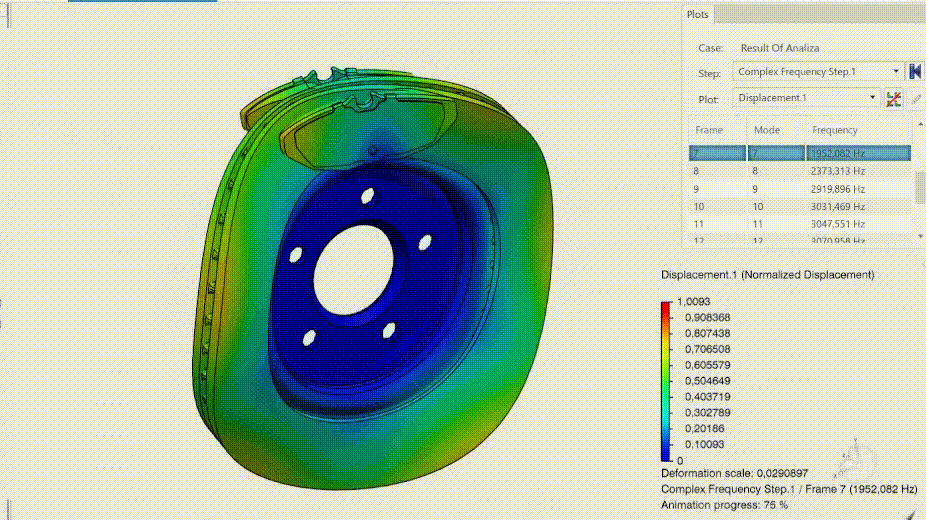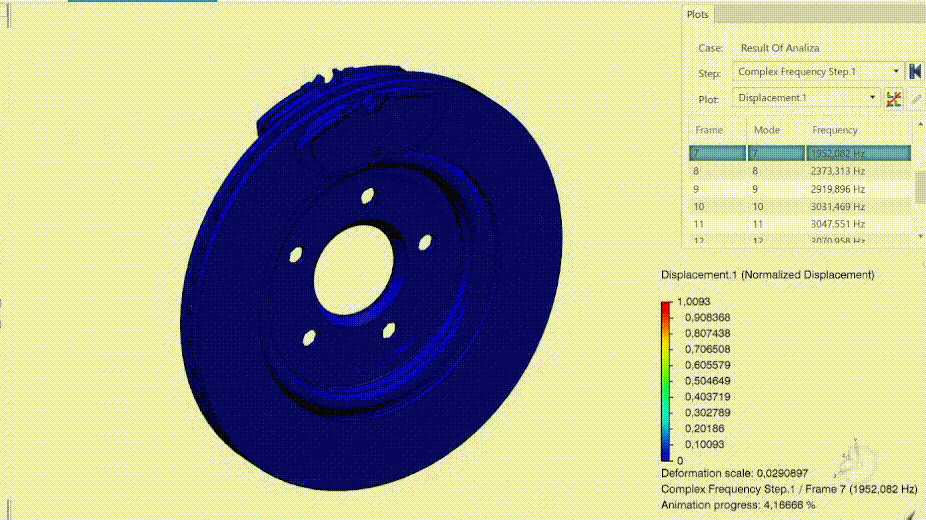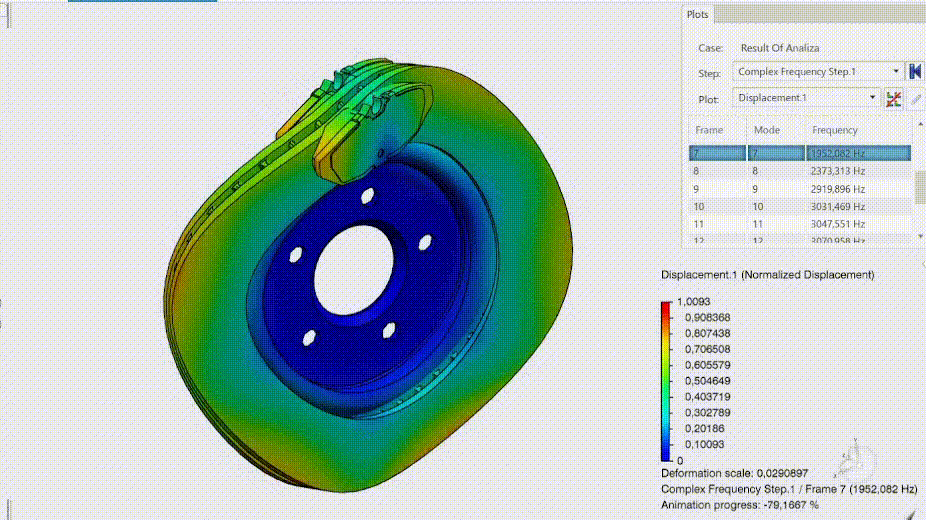
Autor: Rafał Szypulski

Podsumowanie pierwszego dnia 3DEXPERIENCE World 2024

Model Mania 2024 3DEXPERIENCE World

Platforma 3DEXPERIENCE w VLP and Partners

3DEXPERIENCE World 2024

3DEXPERIENCE World 2023: wiodące firmy wskazują drogę do innowacji i chmury

Zmiany w kierownictwie Dassault Systèmes


Zapisywanie dokumentów SOLIDWORKS w postaci poprzednich wersji

Podsumowanie pierwszej oficjalnej konferencji KeyShot w Polsce

Przemysłowa Wiosna 2026 –targi dla przemysłu w sercu Polski

Targi Plastpol. Mocny filar branży w Europie Środkowo – Wschodniej

EZ-CAM – Intuicyjne oprogramowanie CAM

Czym jest PLM?

Wizualizacja danych sił RWIND w programie ParaView











