Analiza liniowego obciążenia krytycznego metodą pasm skończonych (FSM)
Aby umożliwić ocenę wpływu lokalnych zjawisk stateczności smukłych elementów, w programach RFEM 6 i RSTAB 9 można przeprowadzić liniową analizę obciążenia krytycznego na poziomie przekroju. Poniższy artykuł poświęcony jest podstawom obliczeń i interpretacji wyników.
W przypadku stalowych elementów cienkościennych, oprócz globalnego zaniku stateczności (wyboczenie, wyboczenie), należy również zbadać lokalne zachowanie przekroju. W EN 1993-1-3 Patrz [1] rozróżnia się dwa typy:
- Wyboczenie lokalne: Charakteryzuje się wyboczeniem poszczególnych części przekroju poza ich płaszczyzną, przy czym zakłada się przegubowe podparcie naroży przekroju. Ta postać stateczności jest opisana w EN 1993-1-5 Odnieść się [2] jako wyboczenie płyty.
- Całkowite niestabilność pola/niestabilność formy: Charakteryzuje się ominięciem usztywnienia krawędziowego przekroju. Jednocześnie w sąsiednich częściach przekroju zachodzą odkształcenia w płaszczyźnie.
W programach RFEM 6 i RSTAB 9 można obliczać współczynniki obciążenia krytycznego i postacie drgań dla nazwanych lokalnych zjawisk stateczności przy obciążeniu jednostkowym. Obliczenia są liniową analizą stateczności opartą na "Metodzie ograniczonych pasm skończonych (cFSM)" Patrz [3] . Wyniki obliczeń skończonych dla wszystkich przekrojów cienkościennych można wyświetlić w oknie dialogowym "Edytować przekroje". Oprócz naprężeń jednostkowych i innych funkcji przekrojów można użyć menu rozwijanego poniżej widoku przekroju, aby wybrać kształty wyboczenia wywołane obciążeniem jednostkowym (rys. 1).
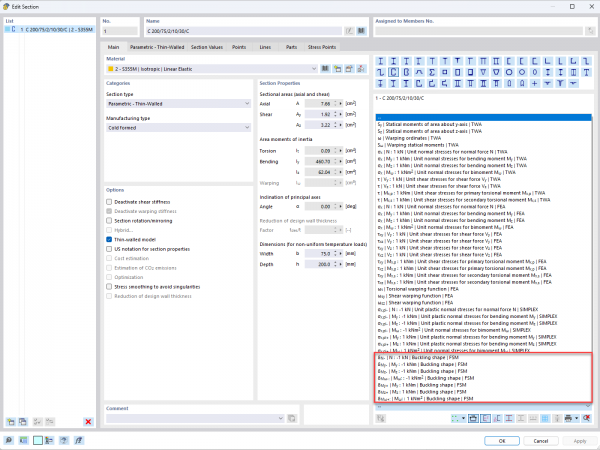
Uzyskiwanie dostępu do wyników FSM
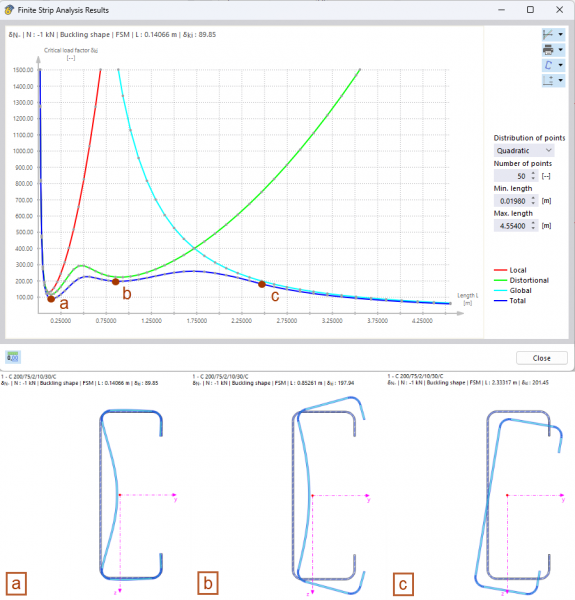
Jeżeli wybrane zostanie jedno z obciążeń jednostkowych, otwiera się interaktywny wykres "Wyniki metody skończonych smug". Przedstawiona niebieska krzywa przedstawia minimalne obciążenie krytyczne w funkcji odpowiedniej połówkowej długości fali wyboczenia. Wyniki można również przedstawić oddzielnie dla różnych postaci stateczności, wyboczenia lokalnego, niestateczności i globalnego zniszczenia stateczności (przy założeniu belki jednoprzęsłowej podpartej widłowo) (rys. 2).
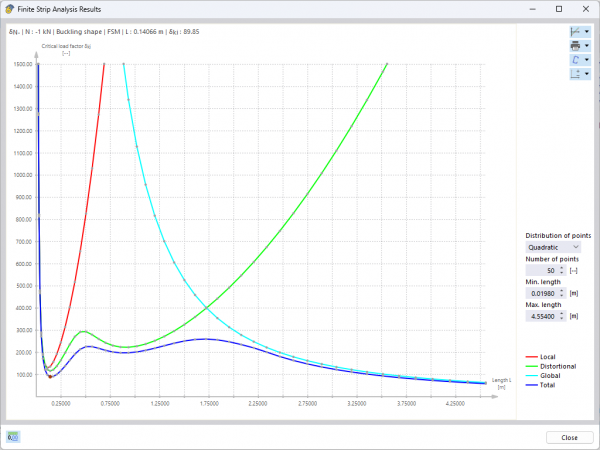
Wykres wyników analizy obciążeń krytycznych
Należy zauważyć, że tylko pierwsza (jednofalowa) postać własna odpowiedniego kształtu stateczności jest brana pod uwagę w analizie stateczności. Wyznaczone obciążenia odgałęzień odnoszą się jednak również do wielokrotności odpowiednich połówkowych długości fali. Można to wykazać za pomocą obliczeń porównawczych z wykorzystaniem elementów powłokowych i dodatku stateczności konstrukcyjnej. Dla badanego przekroju ceowego o długości 0,141 m powoduje to obciążenie krytyczne wynoszące -90,47 kN, co bardzo dobrze zgadza się z wynikiem FSM wynoszącym -89,85 kN (patrz Rysunek 2). Jeżeli długość zostanie podwojona do 0,282 m, liczba wyboczeń również podwaja się przy mniej więcej stałym obciążeniu odgałęzieniami (-91,68 kN). W celu określenia decydujących obciążeń odgałęzień dla lokalnych zjawisk stateczności (wyboczenie lokalne i niestateczność kształtu) należy zawsze uwzględniać odpowiednie minima wyznaczonych krzywych granicznych.
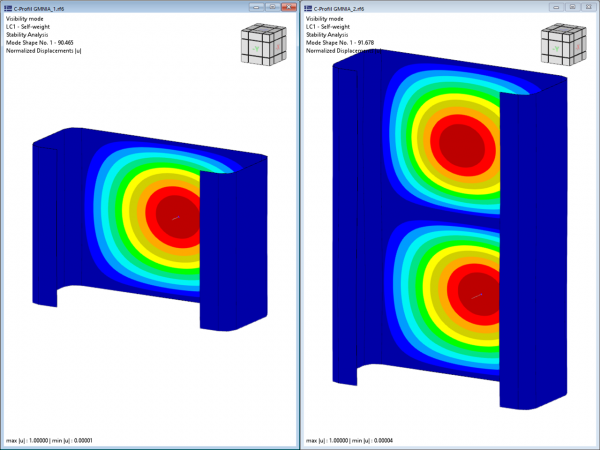
Obliczenia porównawcze na modelu powłokowym z modułem stateczności konstrukcyjnej
Odkształcenia przekroju skojarzone z obliczonym obciążeniem krytycznym można wyświetlić na wykresie przekroju. Domyślnie wyświetlany jest kształt postaci, który należy do pierwszego lokalnego minimum krzywej obciążenia krytycznego. Po „klikaniu” dowolnego punktu danych na wykresie, widok jest automatycznie aktualizowany. Kształty drgań pokazane na rys. 4 wyraźnie pokazują wpływ odpowiednich przebiegów stateczności na wyznaczane obciążenie krytyczne. Podczas gdy w punkcie a dominuje wyboczenie lokalne, postać drgań w punkcie b charakteryzuje się niestatecznością kształtu. W punkcie c widać natomiast przemieszczenie przekroju poprzecznego bryły sztywnej, które jest związane z załamaniem stateczności (tutaj zwichrzenie).
Wyboczenie lokalne, niestateczność kształtu i globalne zniszczenie stateczności
Wyniki analizy FSM umożliwiają wstępną ocenę stateczności smukłych przekrojów i wskazują, czy w przypadku uszkodzenia stateczności dominuje lokalna, globalna interakcja obu form stateczności. Wyznaczone współczynniki obciążenia krytycznego można również wykorzystać do obliczenia granicznej nośności smukłych przekrojów zgodnie z EN 1993-1-3 [1] lub AISI S100-16 [4].
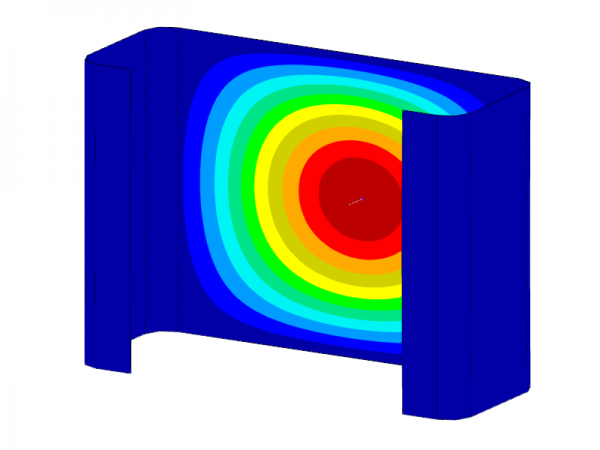
Model powierzchniowy, profil C, jednofazowa klamra
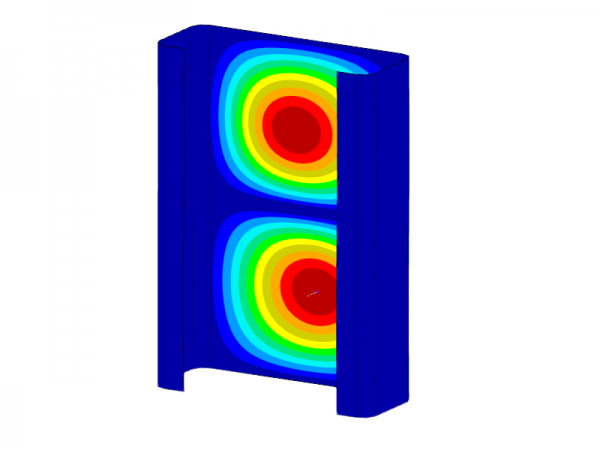 Model powierzchniowy, profil C, kształt podwójnej klamry falistej
Model powierzchniowy, profil C, kształt podwójnej klamry falistej


Zapisywanie dokumentów SOLIDWORKS w postaci poprzednich wersji

Podsumowanie pierwszej oficjalnej konferencji KeyShot w Polsce

Przemysłowa Wiosna 2026 –targi dla przemysłu w sercu Polski

Targi Plastpol. Mocny filar branży w Europie Środkowo – Wschodniej

EZ-CAM – Intuicyjne oprogramowanie CAM

Czym jest PLM?

Wizualizacja danych sił RWIND w programie ParaView